This week we read a paper on Scalable Exact algorithm for Bayesian inference for Big Data by Pollock et al, 2016 [1]. They introduce a Monte Carlo algorithm based on a Markov process with a quasi-stationary distribution that coincides with the distribution of interest. The authors show theoretical guarantees for recovering the correct limiting target distribution using their proposed algorithm. Moreover, they argue that this methodology is practical for big data in which they use a subsampling technique with sub-linear iterative cost as a function of data size.

Background

The problems with current methods like Metropolis Hastings, especially for big data, include:

• They need $O(n)$ calculation at each step for reject/accept decisions,

• They need $O(n)$ new variables when augmenting data.

Hence, modifications are needed when working with big data. Some of the previous solutions include:

• Divide-and-conquer: The weakness of this method is that the recombination of the separately conducted inference is inexact.

• Exact Subsampling: These methods require subsets of the data of random size at each iteration. One approach is to construct unbiased estimators of point-wise evaluations of the target density using subsets of the data, which could then be embedded within the pseudo-marginal MCMC framework. Unfortunately, the construction of such positive unbiased estimators is not possible in general. Another approach is to choose the size of subset such that with high probability the correct decision is made. However, it was shown that such approaches, although cheaper, require subsets of the data of size $O(n)$.

• Approximate subsampling: These methods use a fixed subset of the data at each iteration. One approach is to model it as a Langevin diffusion which has known invariant distribution. Unfortunately, exact simulation from the Langevin diffusion is not possible for general target distribution. Even if possible, evaluation of the drift of the diffusion would be an $O(n)$ calculation. One natural approach would be to employ a stochastic gradient Euler-Maruyama discretisation scheme. Such stochastic gradient approximations are not exact even if we were to use the entire data set at every iteration. In other words, such an approach would, due to the discretisation error, not recover the correct target distribution. To ensure the correct target distribution is obtained, one approach is to embed the discretised dynamics as a proposal within a Markov chain Monte Carlo framework, which leads to the class of Metropolis-adjusted Langevin algorithms. However, it still has $O(n)$ accept/reject step. In other approaches the original naive stochastic gradient has been corrected by using an increasingly fine discretisation with iteration. Although it is shown that this approach recovers (asymptotically) the correct target distribution, the trade-off is a computational cost which increases nonlinearly with diffusion time, and limited model class applicability (at least with any theoretical guarantees).

Rather than building the methodology upon the stationarity of appropriately constructed Markov chains, here the authors develop a novel approach based on the quasi-limiting distribution of suitably constructed stochastically weighted diffusion processes. Their methods allow us to circumvent entirely the Metropolis-Hastings type accept/reject steps, while still retaining theoretical guarantees that the correct limiting target distribution is recovered. Another key component of their approach is the use of control variates (the first use of control variates within an exact method) to reduce the variability of sub-sampling estimators of features of the posterior, but in addition exploits properties and simulation methods.

Model and Theoretical Results

The authors model the problem as a diffusion $X:R \to R^d$ over an infinite-time horizon.

For simplicity of notations, I will assume that $\Lambda$ is identity matrix (keeping in mind that this model works for general $\Lambda$). They specifically use the “Langevin” diffusion with $\nu (x)$ as its invariant distribution as follow:

Transition densities of this model are:

where $w_T(x,y)$ is a Brownian motion (BM) with start $x$ and end $y$. Moreover,

This transition density has the interpretation that we accept with probability of the expected value result. Since this transition probability is not computable due to $\nu$, they introduce a killed/stopped BM (KBM). The transition density of this KBM is:

In the first theorem it is shown that if we choose $\nu$ to be $\pi^2$ where $\pi$ is the probability of interest, then $\lim_{T\to\infty} k_T(x,\cdot) \to \pi(\cdot)$. This means that by simulating from the KBM, we can approximate $\pi$. Therefor, we need to have an unbiased estimate of $\mathbb{E}_{w^{x,y}}[\exp(-\int_{0}^{T}\Phi(X_s) \mathrm{d}s)]$. The authors introduce Path-space Rejection Samplers (PRS) which is a class of rejection samplers operating on diffusion path-space over a finite time horizon. In this method, appropriately weighted finite dimensional subsets of sample paths are drawn from some target measure (in this case $K_T^x$), by means of simulating from a tractable equivalent measure with respect to the target has bounded Randon-Nikodym derivatives. This strategy is used when a point-wise evaluation of a target distribution is not possible, however, the target distribution is bounded by a positive coefficient of a proposal distribution. In that case, we can approximate the target distribution using the proposal distribution.

The Monte Carlo algorithm that they focus on in this paper is an importance sampling variant of the KBM , in which Brownian motion with path-space information is simulated and weighted continuously in time, with evaluations of the trajectory occurring at exponentially distributed times. They call this approach Importance Sampling Killed Brownian motion (IS-KBM) algorithm. The advantage of this approach over KBM is that we can recover for any $t \in [0, \infty)$ a weighted trajectory by halting the algorithm.

After some algebra and multiple reparametrizations, they show that:

where $U$ and $L$ are upper and lower bounds for $\Phi$, respectively. $\kappa$ has a Poisson distribution with parameter $T(U-L)$, and $\eta$ is uniformly selected from interval $[0,T]$.

It could be interpreted that we need to simulate the time until the process hits one of the bounds for the bridge BM. Then, by simulating a Poisson whose rate is proportional to that time interval, we will get the number of data points that need to be examined in that interval. Last, by picking uniformly points in that interval and evaluating $\Phi$ at them, we will get the unbiased estimate that we are after.

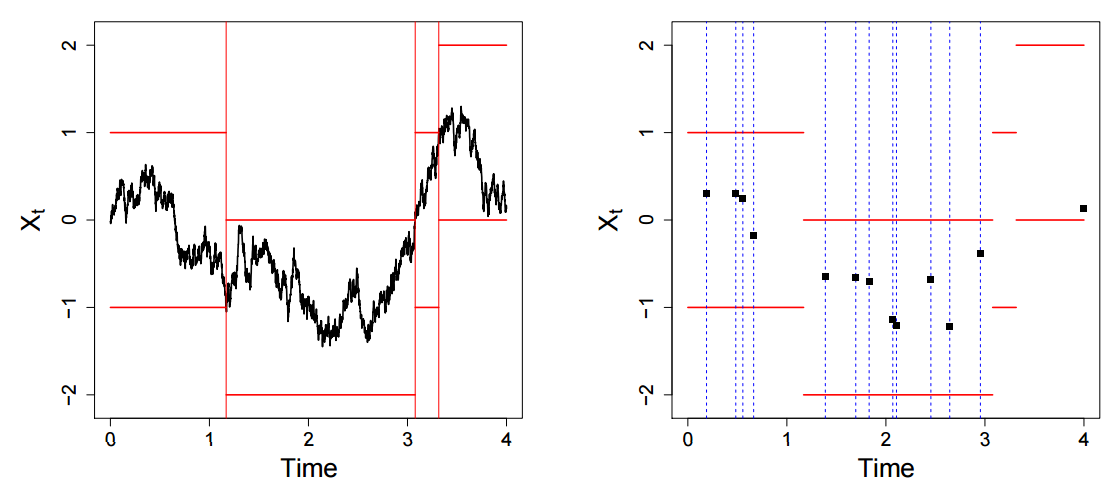
Note that we evaluate the exponential term only at $\kappa$ data points instead of all. The following figure (from Figure 1 of the paper) shows an example for layers simulated for a Brownian motion sample path (left), and Brownian motion sample path simulated as finite collection of event times (right).

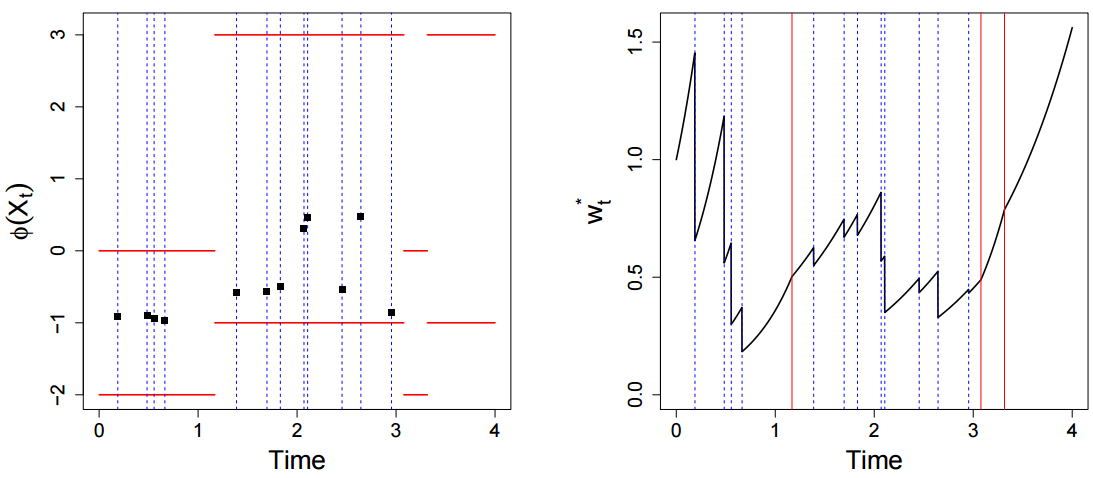
The next figure (also from Figure 1 of the paper) shows the evaluated $\Phi$ function at those points (left) as well as un-normalized importance weight process of sample path, comprising of exponential growth between event times and discrete times at event times.

Although the IS-KBM framework is conceptually appealing, in order to normalize we require a number of trajectories, noting that the variance of the importance sampling weights of these trajectories will increase with time. This means that one sample could have weight $1$ while others have weight $0$. They address this issue using Sequential Monte Carlo (SMC) method in which importance sampling and resampling techniques are combined in order to approximate a sequence of distributions of interest. Hence, they resample at several times (the number of which would be a user chosen threshold). They call this approach Quasi-Stationary Monte Carlo.

One unsolved problem here is evaluation of $\Phi(\cdot)$ which causes $O(n)$ bottleneck within this estimator. They suggest to use $\tilde{\Phi}(.)_A$, $\tilde{U}_X$ and $\tilde{L}_X$ for an auxiliary random variable A (i.e., uniform policy). One issue with this is that initialization of $x$ needs to be within $O(n^{-1/2})$ of the true model.

Discussion

At the end of the reading session, we discussed few points regarding this paper:

• Theoretical methods and analysis offered in this paper are very interesting.
• Altough there is a thorough state-of-the-art review, there is no comparison of this method to other methods such as Bouncy Particle Sampler (BPS).
• The results in experimental sections are all on low-dimensional data sets. SMC is known to have issues with high-dimensional data, and its complexity grows exponentially with dimensionality of data. How does this method perform in higher dimensions?
• Additionally, the initializations of the experiments look quite close to the true model, which might not be easy in general.
• Overall, this was a great paper!

References

[1] Pollock, Murray et al. “The Scalable Langevin Exact Algorithm: Bayesian Inference for Big Data” arXiv preprint arXiv:1609.03436 (2016). link