On our reading list for this week we had the paper by Advani and Ganguli titled “Statistical Mechanics of Optimal Convex Inference in High Dimensions” [1]. Classical statistics gives answers to questions on the accuracy with which statistical models can be inferred in the limits where the measurement density is $\alpha=\frac{N}{P}\rightarrow\infty$ . In this work the authors are concerned with the analyses of the fundamental limits in the finite $\alpha$ regime which is the “big data” regime where both the number of data points $N$ and the number of parameters $P$ tend to infinity but their ratio is still finite.

Statistical Mechanics of Optimal Convex Inference in High Dimensions

For their analysis authors use the ubiquitous statistical inference procedure, regression: $y_{\mu}=X_{\mu}s^{0}+\varepsilon_{\mu}$ . More specifically in their analysis they consider the class of inference algorithms known in the statistics literature as M-estimators:

$\hat{s}=\text{argmin} \left(\sum_{N}\rho(\varepsilon_{\mu})+\sum_{P}\sigma(s_{i}) \right)$

In this setup $\rho=-\log(P(\varepsilon)$ and $\sigma=0$ yields the ML estimate while setting $\rho=-\log(P(\varepsilon))$ and $\sigma=-\log(P(s))$ gives the MAP estimate. As we noted in the reading group this class of estimators doesn’t include Bayesian inference of the posterior mean.

Analysis is focused on the behavior of the error in estimating the signal $q_{s}=\frac{1}{P}\sum_{i=1}^{P}(\hat{s}_{i}-s_{i}^{0})^{2}$ and the noise $q_{\varepsilon}=\frac{1}{N}\sum_{\mu=1}^{N}(\hat{\varepsilon}-\varepsilon_{\mu})^{2}$ .

Review of classical statistics regime where $\alpha\rightarrow\infty$

In classical statistics regime we have the Cramer-Rao (CR) bound which is the lower bound on the error of any unbiased estimator:

$q_{s}\geq\frac{1}{N}\frac{1}{J[\varepsilon]}=\frac{1}{\alpha}\frac{1}{J[\varepsilon]}$

Where, $J[\varepsilon]$ is the Fisher information:

$J[\varepsilon]=\left\langle \left[\frac{\partial}{\partial s^{0}}\log(P(y|s^{0}))\right]^{2}\right\rangle _{y}$

Statistical Mechanics

The general idea is to solve

$\hat{s}=\text{argmin}(\sum_{N}\rho(\varepsilon_{\mu})+\sum_{P}\sigma(s_{i}))$

for generic convex $\rho$ an $\sigma$ by:

Defining a physical system augmented with an inverse temperature $\beta$ whose ground state is a solution to the problem as $\beta\rightarrow\infty$ . The energy in terms of $u=s^{0}-s$ is:
$E(u)=\sum_{N}\rho(\varepsilon_{\mu}+X_{\mu j}u_{j})+\sum_{P}\sigma(s_{j}^{0}-u_{j})$
Calculating the free energy of the system using the replica trick.

A physical system in the micro-canonical ensemble minimizes $E$ . A physical system in the canonical ensemble (held at constant temperature $\frac{1}{\beta}$ ) minimizes the free energy:
$F=E-TS=\left\langle -\log(Z)\right\rangle =\left\langle -\log(\int \mathrm{d}u e^{-\beta E(u)})\right\rangle.$
Taking the $\beta\rightarrow\infty$ limit.

The general idea of the replica trick is to calculate an average over a polynomial of $Z$ instead of an intractable function of $Z$ . The free energy is calculated using:
$F=-\left\langle \log Z\right\rangle = \lim_{n\rightarrow 0}\left\langle \frac{Z^{n}-1}{n}\right\rangle =\lim_{n\rightarrow 0} \left\langle \frac{\partial Z^{n}}{\partial n}\right\rangle$
Where $Z^{n}$ is the partition function of $n$ “copies” of the system. The integral over $X$ , $s^{0}$ and $\varepsilon$ couples these copies. This interpretation is valid for integer $n$ , but the formula is taken to hold for continuous $n$ . We get:
$\left\langle Z^{n}\right\rangle = \left\langle \int \prod_{a=1}^{n} \mathrm{d}u^{a} e^{-\sum_a \beta E(u^{a})} \right\rangle = \int \prod_{a,b=1}^{n} \mathrm{d}Q_{ab} \mathrm{d}\hat{Q}_{ab} e^{-Nf(Q,\hat{Q})}$
Where
$Q_{ab}\delta_{\mu\nu} = \left\langle X_{\mu}\cdot u^{a}X_{\nu}\cdot u^{b} \right\rangle_{X}$

In the replica symmetric (RS) approximation the assumption is that the $2n^{2}$ variables $Q_{ab},\hat{Q}_{ab}$ can be replaced by four variables in the form $Q=\text{diag}(\Delta)+ \mathbb{1}(Q_{0})$ . This is a mean field assumption on the interaction between the replicas. Details about the validity of this assumption are given in [2]. The results are:

$q_{d}=\frac{\left\langle\left\langle M'_{\lambda_{\rho}}[\rho](\varepsilon_{q_{s}})^{2}\right\rangle\right\rangle_{\varepsilon_{q_{s}}}}{\alpha\left\langle\left\langle M''_{\lambda_{\rho}}[\rho](\varepsilon_{q_{s}})\right\rangle\right\rangle _{\varepsilon_{q_{s}}}^{2}}$ $q_{s}=\left\langle\left\langle (\hat{s}(s_{q_{s}}^{0})-s^{0})^{2}\right\rangle\right\rangle _{s_{q_{d}}^{0}}$ $1-\frac{1}{\alpha}\frac{\lambda_{\rho}}{\lambda_{\sigma}}=\left\langle\left\langle \hat{\varepsilon}'(\varepsilon_{q_{s}})\right\rangle\right\rangle _{\varepsilon_{q_{s}}}$ $\frac{\lambda_{\rho}}{\lambda_{\sigma}}=\left\langle\left\langle \hat{s}'(s_{q_{d}}^{0})\right\rangle\right\rangle _{s_{q_{d}}^{0}}$

Where:

$\varepsilon_{q_{s}}=\varepsilon+\sqrt{q_{s}}z_{\varepsilon}, s_{q_{s}}^{0}=s^{0}+\sqrt{q_{d}}z_{s}$ $\hat{\varepsilon}(\varepsilon_{q_{s}})=P_{\lambda_{\rho}}[\rho](\varepsilon_{q_{s}}), \hat{s}(s_{q_{d}}^{0})=P_{\lambda_{\sigma}}[\sigma](\varepsilon_{q_{d}})$ $\left(\mathcal{E}_{gen}=\left\langle \varepsilon_{q_{s}}^{2}\right\rangle =q_{s}+\left\langle \varepsilon\right\rangle ^{2}, \mathcal{E}_{train}=\left\langle \hat{\varepsilon}(\varepsilon_{q_{s}})^{2}\right\rangle \right)$

Inference Without Prior Information

If we can’t utilize prior information, then we set $\sigma=0$ which gives $\hat{s}(s_{q_{d}}^{0})=s_{q_{d}}^{0}$ and the equations reduce to:

$q_{s}=q_{d}=\frac{1}{\alpha}\frac{\left\langle (M'[\rho])^{2}\right\rangle _{\varepsilon_{q_{s}}}}{\left\langle M''[\rho]\right\rangle _{\varepsilon_{q_{s}}}^{2}}$

Optimal error in the finite $\alpha$ regime

What is the optimal error in this setting? We can rewrite the equations as:

$\alpha\left\langle (\lambda_{\rho}M_{\lambda_{\rho}}[\rho]'(\varepsilon_{q_{s}}))^{2}\right\rangle -q_{s}=0\equiv A$ $\alpha\left\langle \lambda_{\rho}M_{\lambda_{\rho}}[\rho](\varepsilon_{q_{s}})''\right\rangle -1=0\equiv B$

Then after some algebra that eliminates the $\lambda_{\rho}M_{\lambda_{\rho}}[\rho]'(\varepsilon_{q_{s}})$ terms we can obtain:

$q_{s}^{opt}=\frac{1}{\alpha}\frac{1}{J[\varepsilon_{q^{opt}}]}\geq\frac{1}{(\alpha-1)J[\varepsilon]}$

Notice that the bound is higher than the Cramer-Rao bound due to the additional noise added to $\varepsilon$ from $z$ .

Optimal cost

One can look for $\rho_{opt}$ that achieves $q_{opt}$ by adding these constraints to a Lagrangian that minimizes the error:

$L=q_{s}-\lambda A-\mu B$

Then by solving the Euler-Lagrange equation $\frac{\partial L}{\partial r}-\frac{\partial}{\partial y}\frac{\partial L}{\partial r'}=0$ , and inverting the Moreau envelope $M[f]=g\Leftrightarrow f=-M[-g]$ we obtain:

$\rho_{opt}=-M_{q_{opt}}[\log(f_{q_{opt}})]=-M_{q_{opt}}[-E_{q_{opt}}]$

Where $f_{q_{opt}}$ is the PDF of $\varepsilon_{q_{opt}}$ .

Figure 4 from the paper (shown below) gives a comparison summary of the generalization (a) and training (b) error of the optimal unregularized M-estimator with ML and quadratic loss functions. It shows over-fitting as $\alpha\rightarrow1$ . Optimizing over $q_{s}$ is analogous to optimizing over $\mathcal{E}_{gen}=q_{s}+\left\langle \varepsilon^{2}\right\rangle$ and not $\mathcal{E}_{train}=\left\langle \hat{\varepsilon}(\varepsilon_{q_{s}})^{2}\right\rangle$ .

Fig. 4 in the paper

Inference With Prior Information

We start with the often used quadratic loss and regularization: $\rho(x)=\frac{1}{2}x^{2}$ , and $\sigma(x)=\frac{1}{2}\gamma x^{2}$ .

As we have seen, for $f=\frac{1}{2}\gamma x^{2}$ we have the simplification:

$P[f](x)=\text{arg} \min_y \left[\frac{1}{2\lambda}(x-y)^{2}+\frac{1}{2}\gamma y^{2} \right]=\frac{x}{1+\gamma\lambda}$

The four equations reduce to:

$\frac{q_{d}}{\lambda_{\sigma}^{2}}=\frac{\alpha}{(1+\lambda_{\rho})^{2}}\left\langle\left\langle \varepsilon_{q_{s}}^{2}\right\rangle\right\rangle _{\varepsilon_{q_{s}}}$ $q_{s}=\left\langle\left\langle \left(\frac{s^{0}+z\sqrt{q_{d}}}{1+\gamma\lambda_{\sigma}}-s^{0}\right)^{2}\right\rangle\right\rangle _{s^{0},z}$ $\lambda_{\sigma}=\frac{1+\lambda_{\rho}}{\alpha}$ $\lambda_{\rho}=\frac{\lambda_{\sigma}}{1+\gamma\lambda_{\sigma}}$

From the first two equations one obtains:

$\bar{q}_{s} = \frac{q_{s}}{\left\langle s_{0}^{2}\right\rangle} =\frac{\phi+\alpha(\gamma\lambda_{\sigma})^{2}}{\alpha(1+\gamma\lambda_{\sigma})^{2}-1}$

The optimal regularization is given by solving $\frac{\partial\bar{q}_{s}}{\partial\gamma}=0$ , which gives $\gamma=\phi$ . This means that high SNR requires little regularization. Plugging this into the remaining equations, we solve for $\bar{q}_{opt}$ :

${\bar{q}_{s}}^{Quad}=\frac{1-\alpha-\phi+\sqrt{(\phi+\alpha-1)^{2}+4\phi}}{2}$

This exhibits a phase transition, which in high SNR reduces to:

if $\alpha \lt 1$ : $\bar{q}_s^{Quad} = 1-\alpha$
if $\alpha = 1$ : $\bar{q}_s^{Quad}= \frac{1}{\sqrt{SNR}}$
if $\alpha \gt 1$ : $\bar{q}_s^{Quad}= \frac{1}{SNR(\alpha-1)}$

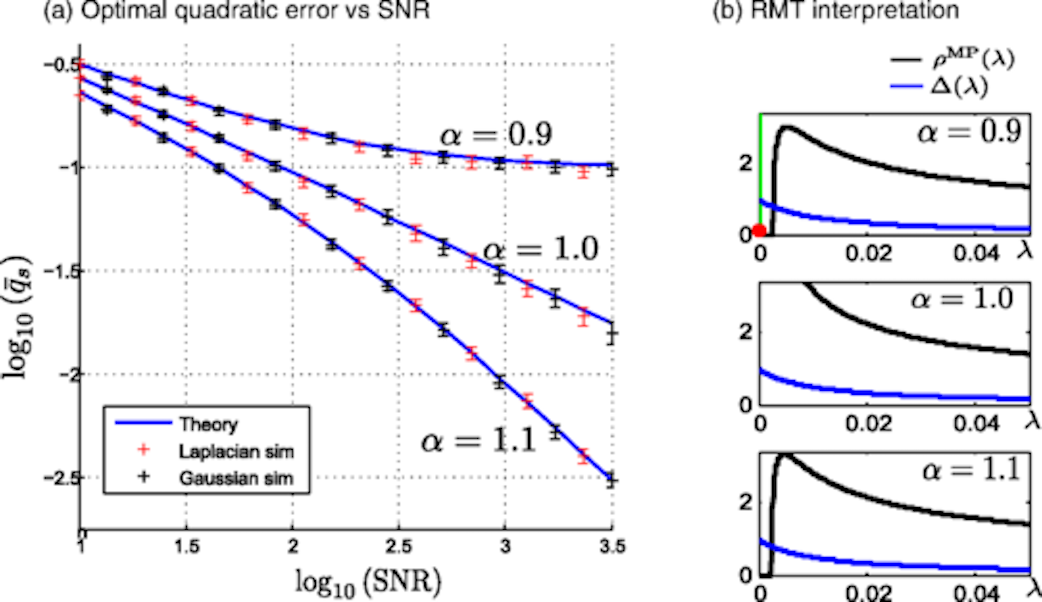
Shown below is Figure 5 from the paper where we observe that $\bar{q}_s^{Quad}$ approaches a constant when $\alpha \lt 1$ .

Fig. 5 in the paper

Optimal Inference with non-Gaussian Signal and Noise

Generalizing the unregularized case, the optimal cost and regularizer is found to be:

$\rho_{opt}=-M_{ {q_{s}}^{opt}}[\log(P_{\varepsilon_{ {q_{s}}^{opt}}})]$ $\sigma_{opt}=-M_{ {q_{d}}^{opt}}[\log(P_{s_{ {q_{d}}^{opt}}}]$

Where:

${q_{d}}^{opt}=\frac{1}{\alpha J[\varepsilon_{ {q_{s}}^{opt}}]}, {q_{s}}^{opt}={q_{s}}^{MMSE}({q_{d}}^{opt})$

References

[1] Madhu Advani and Surya Ganguli. “Statistical mechanics of optimal convex inference in high dimensions”, In Physical Review X, 6:031034 (2016). link

[2] Advani, Madhu, Subhaneil Lahiri, and Surya Ganguli. “Statistical mechanics of complex neural systems and high dimensional data.” Journal of Statistical Mechanics: Theory and Experiment 2013.03 (2013): P03014. link

Columbia Advanced Machine Learning Seminar

Statistical Mechanics of Optimal Inference in High Dimensions

Statistical Mechanics of Optimal Convex Inference in High Dimensions

Review of classical statistics regime where $\alpha\rightarrow\infty$

Statistical Mechanics

Inference Without Prior Information

Inference With Prior Information

Optimal Inference with non-Gaussian Signal and Noise

References

Statistical Mechanics of Optimal Convex Inference in High Dimensions

Review of classical statistics regime where \alpha\rightarrow\infty

Statistical Mechanics

Inference Without Prior Information

Inference With Prior Information

Optimal Inference with non-Gaussian Signal and Noise

References

Review of classical statistics regime where $\alpha\rightarrow\infty$