This week Robin led our discussion of two papers - “Value Iteration Networks” by Tamar et al., which won Best Paper at NIPS 2016, and “Unsupervised learning for physical interaction through video prediction” by Finn et al, also from NIPS 2016. The former introduces a novel connection between convolutional architectures and the value iteration algorithm of reinforcement learning, and presents a model that generalizes better to new tasks. The latter introduces a number of architectures for video prediction. A common theme in both papers is the exploitation of local structure in the problem in order to simplify the resulting calculations.
The figures and tables below are copied from the aforementioned papers.
Value Iteration Networks
Reinforcement learning
The basic framework in which reinforcement learning is studied is the Markov Decision Process (MPD). This is a tuple | of (respectively) discrete states, actions, rewards that are a function of the state and a transition kernel giving the probability of the process reaching state at time if it is in state at time and takes action . The objective of reinforcement learning is to obtain a policy that chooses the optimal action to take from every state so as to maximize the cumulative expected reward starting from a given state, known as the value
where is a discount factor that captures the notion of diminishing returns due to the inherent uncertainty of future rewards. There are also alternative frameworks where instead of using discounted rewards one truncates the sum over at some finite , or when a certain goal state (or states) is reached. The average is over the state and action trajectories generated by and . As discussed in [3], if the exact state of the system is known at all times a dynamic programming approach can be used to find the optimal policy * that maximizes . This is done by the value iteration algorithm, an iteration of which comprises the following steps
This process is known to converge to the optimal value * (and a corresponding *). The optimal policy is then given by **.
An important generalization of the standard MDP is the partially observed MPD (POMDP) where instead of having access to the state, the agent receives only a noisy observation of the state . The deterministic policy discussed above is then replaced by a parameterized probability distribution over actions conditioned on these observations |.
The standard reference for reinforcement learning, where other extensions of this framework and algorithms to solve such problems are discussed, is Sutton & Barto [3].
Reinforcement learning and neural networks
The use of ideas and architectures developed for supervised learning in problems of reinforcement learning has been a common theme in recent years. Some of the most well known examples of this trend have been the works where neural networks were trained to play Atari games [4] and Go [5]. These results are based on networks known as DQNs, which parameterize the policy and value functions of reinforcement learning using deep neural networks.
The innovation of the current work is the realization that a step of the value iteration algorithm is identical to the operation performed by a convolutional block in a convolutional neural network (CNN). The value function takes the place of the input to the layer, while | form the weights of | | convolution channels. In many tasks of interest such as grid world navigation, | reflects the locality of the problem since transitions are only possible to nearby states. This is analogous to the locality of convolutional kernels in standard CNNs, which is useful due to the hierarchical structure in natural images.
Due to this connection, value iteration can be performed by a differentiable VI block that is composed of recursively connecting such convolutional blocks. One must then choose in such a way as to ensure convergence while not incurring a high computational cost by setting it to be too large. Due to the differentiable nature of the block, the entire resulting network can then be trained using standard backpropagation. It is shown empirically that such value iteration networks “learn to plan” and can thus generalize from one task to another better than other existing architectures.
The architecture is illustrated in the following figure:
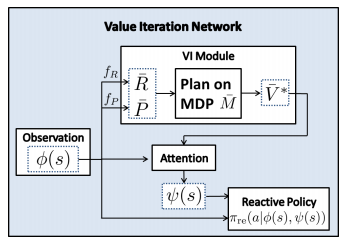
Experiments
Imitation learning is a supervised learning problem where the optimal policy for a novel task is learned through a set of observations of optimal actions and states in related tasks. The tasks could be grid world navigation in different landscapes that are generated from the same distribution. In such experiments the VIN architecture generalizes better than other convolutional architectures that are more similar to those in the works. Other experiments include a discretized versions of problems with continuous state spaces where the above formalism cannot be directly applied, as well as a web navigation task that generalizes the 2D state space of the previous experiments. In all the experiments the VIN outperformed competing architectures.
The results for the grid world experiment are shown below. Note the higher success rate of the Value Iteration Network compared to architectures based on convolutional networks without the VI module. The performance gap is bigger for larger grids. The trajectory difference is a measure of the difference between the trajectory predicted by the network and the optimal shortest path to the goal.

Discussion
One point that arose in the discussion is the choice of the number of iterations . While this was chosen to scale with the grid size for the grid world examples it is unclear if there is a general way to choose this parameter for novel tasks. Another interesting possible extension of the work that was discussed is the use of different operations instead of max pooling in the VI module. The use of softmax, for instance, would lead to the output of a single iteration being a distribution of values for different actions instead of a single . In order to prevent an exponential growth in the size of the network one could only consider the likeliest values as in beam search.
Unsupervised Learning for Physical Interaction through Video Prediction
This paper presents a number of related architectures for the purpose of unsupervised video prediction. The algorithm receives a series of video frames at times as input and must predict the frame at time .
DNA and CDNA
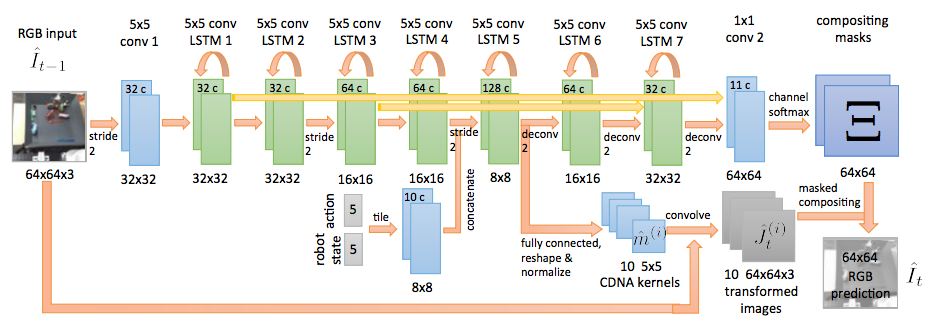
The idea behind the Dynamic Neural Advection (DNA) network is to generate a local, highly non-linear motion transformation matrix for each pixel of the new image. This is a matrix for some < where the original image is . This assumption of locality is motivated by the fact that individual pixels cannot move too far across the image between frames, and as a result the dimensionality of the problem is reduced. is generated by a convolutional neural network with LSTM cells connecting the different convolutional layers. The new image predictor is then given by
Convolutional Dynamic Neural Advection (CDNA) is a convolutional variation of this architecture where are uniform across the image, and are replaced by a set where indexes the convolution channels. This generates a set of predictions
which are modulated with a mask that weights the different channels to give the image prediction .
The CDNA architecture is illustrated below:
A third architecture, Spatial Transformer Predictions, replaces the masks with a set of affine transformations as in a Spatial Transformer Network. These are then combined with a bilinear kernel to give a set of predictions as follows:
and the predictions from the different channels are then combined with a mask as in the case of the CDNA.
While it may appear that these algorithms only explicitly rely on the previous time step to make predictions, information about previous time steps is stored in the LSTM cells.
Experiments
For the purpose of testing the models, a new dataset of 1.5 million video frames of robots interacting with objects. The Peak Signal to Noise Ratio (PSNR) metric used is introduced in [6] and measures the peak SNR between the ground truth and the predicted frame. The SSIM metric is discussed in [7]. All the proposed architectures outperformed existing architectures on these tasks. The models were able to produce plausible predictions for up to 10 time steps, corresponding to about 1 second of video. The results for video prediction on the robot interaction dataset is shown below.

The CDNA and STP variants are able to capture correlated motion of different pixels that correspond to objects, as can be seen below for instance in the generated affine masks. The DNA architecture on the other hand can model independent motion for different pixels and is thus less interpretable but more flexible.

References
[1] Tamar, Aviv, et al. “Value iteration networks.” Advances in Neural Information Processing Systems. 2016. link
[2] Finn, Chelsea, Ian Goodfellow, and Sergey Levine. “Unsupervised learning for physical interaction through video prediction.” Advances In Neural Information Processing Systems. 2016. link
[3] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. Vol. 1. No. 1. Cambridge: MIT press, 1998.
[4] Mnih, Volodymyr, et al. “Human-level control through deep reinforcement learning.” Nature 518.7540 (2015): 529-533. link
[5] Silver, David, et al. “Mastering the game of Go with deep neural networks and tree search.” Nature 529.7587 (2016): 484-489. link
[6] Mathieu, Michael, Camille Couprie, and Yann LeCun. “Deep multi-scale video prediction beyond mean square error.” arXiv preprint arXiv:1511.05440 (2015). link
[7] Wang, Zhou, et al. “Image quality assessment: from error visibility to structural similarity.” IEEE transactions on image processing 13.4 (2004): 600-612. link