This week Christian led our discussion of two papers relating to MCMC: “A Complete Recipe for Stochastic Gradient MCMC” (Ma et al. 2015) and “Relativistic Monte Carlo” (Lu et al. 2017). The former provides a general recipe for constructing Markov Chain Monte Carlo (MCMC) samplers—including stochastic gradient versions—based on continuous Markov processes, thus unifying and generalizing earlier work. The latter presents a version of Hamiltonian Monte Carlo (HMC) based on relativistic dynamics that introduce a maximum velocity on particles. It is more stable and robust to the choice of parameters compared to the Newtonian counterpart and shows similarity to popular stochastic optimizers such as Adam and RMSProp.

The figures and tables below are copied from the aforementioned papers or posters.

A Complete Recipe for Stochastic Gradient MCMC

Background

The standard MCMC goal is to generate samples $\theta_i$ from posterior distribution $p(\theta|\mathcal{D})$. Recent efforts focus on designing continuous dynamics that leave $p(z|\mathcal{D})$ as the invariant distribution. The target posterior is translated to an energy landscape $H(z)$ that gradient-based dynamics explore: $p(z|\mathcal{D})\propto \exp(-H(z))$, where $z=(\theta,r)$ with auxiliary variables $r$, e.g. the momentum in HMC. How does one define such continuous dynamics?

Recipe

All continuous Markov processes that one might consider for sampling can be written as a stochastic differential equation (SDE) of the form:

where $f(z)$ denotes the deterministic drift, $W(t)$ is a $d$-dimensional Wiener process, and $D(z)$ is a positive semidefinite diffusion matrix. The paper proposes to write $f(z)$ directly in terms of the target distribution:

Here, $Q(z)$ is a skew-symmetric curl matrix representing the deterministic traversing effects seen in HMC procedures. In contrast, the diffusion matrix $D(z)$ determines the strength of the Wiener-process-driven diffusion. $\epsilon$-discretization yields a practical algorithm, which is basically preconditioned gradient decent with the right amount of additional noise injected at each step.

The authors prove that sampling the stochastic dynamics of Eq. (1) with $f(z)$ as in Eq. (2) leads to the desired posterior distribution as the stationary distribution. They further prove completeness, i.e. for any continuous Markov process with the desired stationary distribution, $p^s(z)$, there exists an SDE as in Eq. (1) with $f(z)$ defined as in Eq. (2). For scalability to large data sets, computing gradient estimates on minibatches already introduces some amount of noise, which has to be estimated such that the additionally injected noise can be appropriately reduced.

Examples

The recipe can be used to “reinvent” previous MCMC algorithms, such as Hamiltonian Monte Carlo (HMC, [3]), stochastic gradient Hamiltonian Monte Carlo (SGHMC, [4]), stochastic gradient Langevin dynamics (SGLD, [5]), stochastic gradient Riemannian Langevin dynamics (SGRLD, [6]) and stochastic gradient Nose-Hoover thermostats (SGNHT, [7]). The corresponding choices of $Q$ and $D$ are listed in following table.

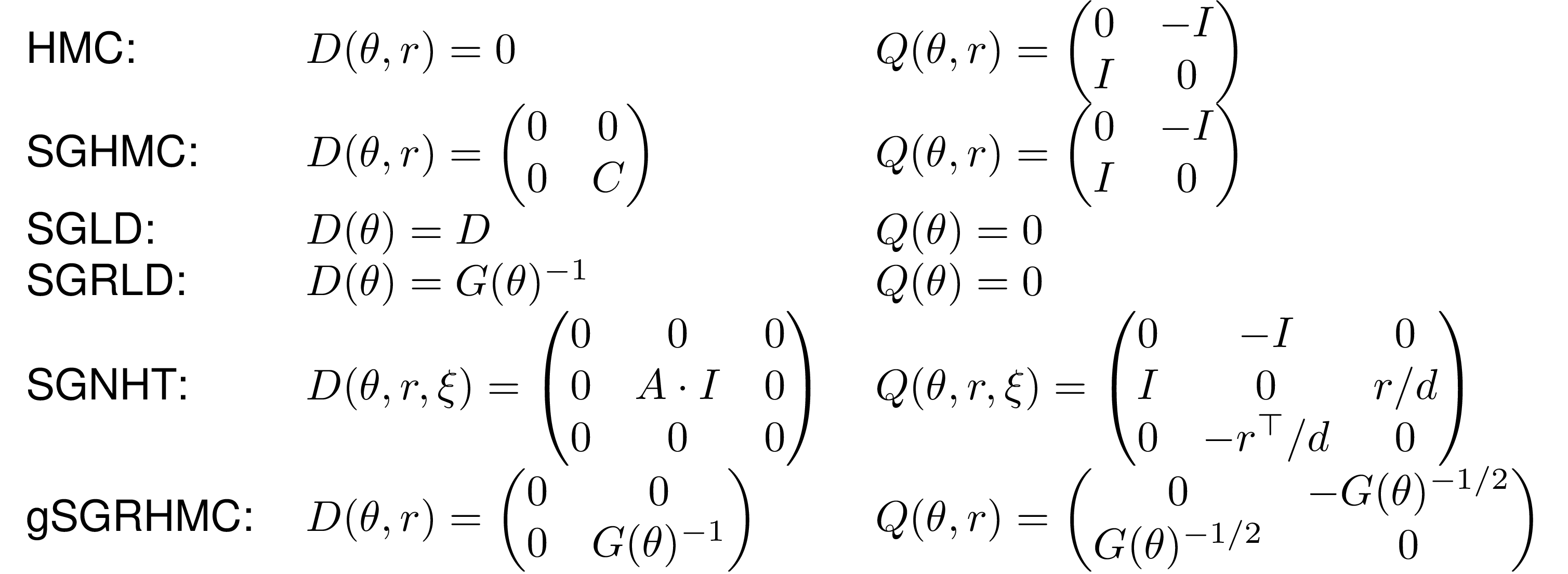
They use the framework to derive a new sampler, generalized stochastic gradient Riemann Hamiltonian Monte Carlo, a state-dependent version of SGHMC, that utilizes the underlying geometry of the target distribution. The corresponding matrices $D$ and $G$ are listed in the table, where $G$ is any positive definite matrix, e.g. the Fisher information metric. The figure shows that gSGRHMC can excel at rapidly exploring distributions with complex landscapes and illustrates its scalability by applying it to a latent Dirichlet allocation model on a large Wikipedia dataset.

Discussion

The authors only considered continuous Markov processes, hence their “complete” recipe is restricted too those. They do not provide details on how to estimate the additional noise of stochastic gradient algorithms operating on data minibatches. The results were apparently already known in the physics literature about the Fokker-Planck equation. Nevertheless, the paper introduces them to the Machine Learning community and nicely unifies recent MCMC papers.

Relativistic Monte Carlo

Background

HMC is sensitive to large time discretizations and the mass matrix of HMC is hard to tune well. In order to alleviate these problems the authors of the second paper propose relativistic Hamiltonian Monte Carlo (RHMC), a version of HMC based on relativistic dynamics that introduce a maximum velocity on particles.

Relativistic MCMC

They replace the Newtonian kinetic energy $\frac{1}{2m}p^\top p$, with “rest mass” $m$ and momentum $p$, by $m c^2\sqrt{\frac{p^\top p}{m^2c^2}+1}$ as in special relativity. The “speed of light” $c$ controls the maximum speed and $m$ the typical speed. Proceeding analogously to standard Newtonian HMC (NHMC), the resulting dynamics are given by Hamilton’s equations and simulated using leapfrog steps with step size $\epsilon$. While the momentum may become large with peaked gradients, the size of the parameter update is $\Delta\theta=\epsilon p \left(\frac{p^\top p}{c^2}+m^2\right)^{-1/2}$ and thus bounded by $\epsilon c$. This also provides a recipe for choosing the parameters $\epsilon$, $c$ and $m$; first the discretization parameter $\epsilon$ needs to be set, then we choose the maximal step $\epsilon c$ and in relation we choose the “cruising speed” by picking $m$. The authors also develop relativistic variants of SGHMC and SGNHT making use of the framework presented in the first paper. Taking the zero-temperature limit of the relativistic SGHMC dynamics yields a relativistic stochastic gradient descent algorithm. The obtained updates are similar to RMSProp [8], Adagrad [9] and Adam [10], with the main difference being that the relativistic mass adaptation uses the current momentum instead of being separately estimated using the square of the gradient.

Examples

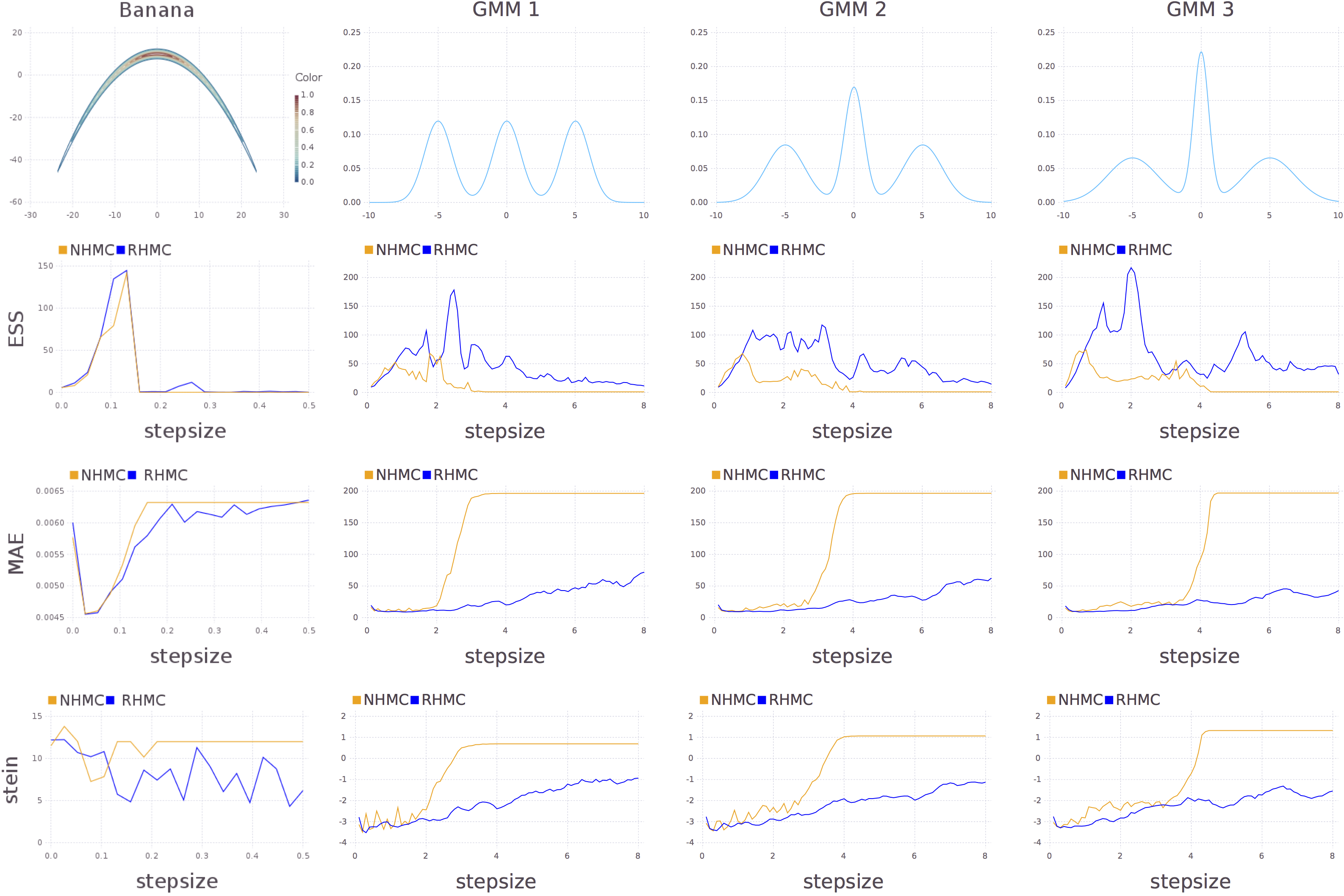
In the performed sampling experiments RHMC achieves similar or slightly better performance than NHMC and is strikingly more robust to the step size. The figure compares the performances of NHMC and RHMC for a wide range of stepsizes, via the effective sample sizes (ESS, higher better), the mean absolute error (MAE) between the true probabilities and the histograms of the sample frequencies (lower better), and the log Stein discrepancy (lower better).

The relativistic stochastic gradient descent algorithm is competitive with Adam on the standard MNIST dataset for deep networks and is able to achieve a lower error rate for an architecture with a single hidden layer.

Discussion

Has Radford Neal really not thought or just not bothered about relativistic HMC?

References

[1] Y. Ma, T. Chen, and E.B. Fox. A Complete Recipe for Stochastic Gradient MCMC. In Advances in Neural Information Processing Systems 28, 2015. link

[2] X. Lu, V. Perrone, L. Hasenclever, Y.W. Teh, S.J. Vollmer. Relativistic Monte Carlo. To appear in AISTATS, 2017. link

[3] R.M. Neal. MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo, 2010.

[4] T. Chen, E.B. Fox, and C. Guestrin. Stochastic gradient Hamiltonian Monte Carlo. In Proceeding of the 31st International Conference on Machine Learning, 2014. link

[5] M. Welling and Y.W. Teh. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th International Conference on Machine Learning, 2011. link

[6] S. Patterson and Y.W. Teh. Stochastic gradient Riemannian Langevin dynamics on the probability simplex. In Advances in Neural Information Processing Systems 26, 2013. link

[7] N. Ding, Y. Fang, R. Babbush, C. Chen, R.D. Skeel, and H. Neven. Bayesian sampling using stochastic gradient thermostats. In Advances in Neural Information Processing Systems 27, 2014. link

[8] T. Tieleman and G. Hinton. Lecture 6.5-RMSProp: Divide the gradient by a running average of its recent magnitude, 2012. COURSERA: Neural Networks for Machine Learning. link

[9] J. Duchi, E. Hazan, and Y. Singer. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J Mach Learn Res, 12:2121–2159, 2011. link

[10] D.P. Kingma and J. Ba. Adam: A method for stochastic optimization. In ICLR, 2015 link