In this week’s session, Yixin led our discussion of two papers about Generative Adversarial Networks (GANs). The first paper, “Generalization and Equilibrium in Generative Adversarial Nets” by Arora et al. [1], is a theoretical investigation of GANs, and the second paper, “Improved Training of Wasserstein GANs” by Gulrajani et al. [2], gives an new training method of Wasserstein GAN. This video gives a good explanation of the first paper.

All images below are copied from the two papers.

GANs and Wasserstein GANs

GAN training is a two-player game in which the generator minimizes the divergence between its generative distribution and the data distribution while the discriminator tries to distinguish the samples from the generator’s distribution and the real data samples. We say the generator “wins” when the discriminator performs no better than random guess.

The optimization problem of the basic GAN is a min-max problem,

In another understanding, the best discriminator gives a divergence measure between the generator’s distribution $G(h), h \sim p_{Normal}$, and the data distribution, $p_{data}$. If we have $p_{data}(x)$ and the discriminator is allowed to be any function, then the generator is optimized to minimize the Jensen-Shannon divergence between $p_{data}$ and $G(h)$.

In practice, people have used Wasserstein distance to measure the divergence between two distributions (See Robin’s post on Wasserstein GANs). The Wasserstein distance between the data distribution and the generative distribution is

where $\mathcal{L}_1$ denotes the set of 1-Lipschitz functions. Here the $f$ is the discriminator and takes the form of neural network. It is learned from GAN training. The objective is to minimize the Wasserstein distance between these two distributions.

The first paper addresses the following problems:

1. The divergence measure is defined on distributions, but what results do we have when the objective is calculated with finite samples?
2. Can the training reach equilibrium?
3. What does “reaching an equilibrium” even mean?

The second paper works on the problem of penalizing the optimizer so that it finds the optimal discriminator approximately in the 1-Lipschitz space.

Generalization and Equilibrium in GANs (Paper 1)

Generalization of the distance measure

Arora et al [1] introduce a new distance measure: the neural network divergence. The distance is defined on distributions that are generated by neural networks.

Theorem: when the sample size is large enough, the distance between two distributions can be approximated by the distance between their respective samples.

Equilibrium

Intuition: a powerful generator is always able to win when it can use an infinite number of mixture components to approximate the data distribution. A less powerful generator with finite but large enough number of mixture component can approximately win the game.

Setup of the game: $u$ and $v$ represent pure strategies of the generator and the discriminator. The payoff $F(u, v)$ of the game is the GAN objective.

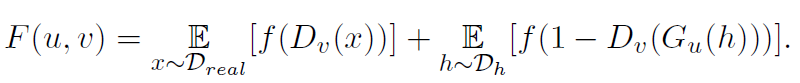
Due to a theorem by von Neumann, the mixed strategy always admits equilibrium, but in this ideal case both the generator and the discriminator need to consider infinite number of pure strategies. The paper proposes $\epsilon$-approximate equilibrium for finite pure strategies.

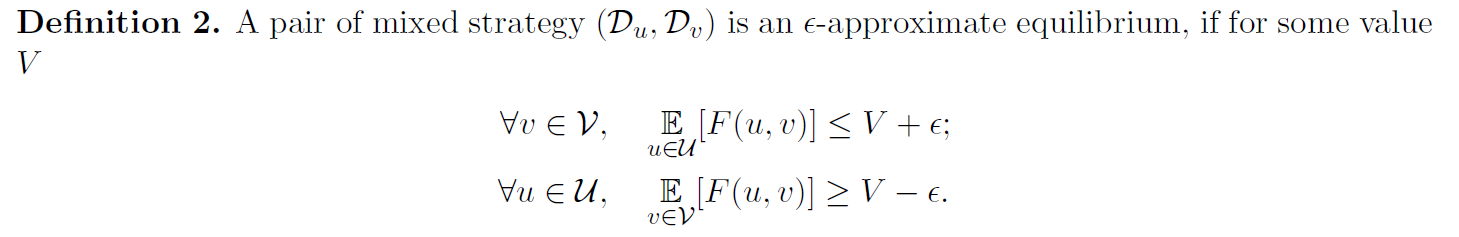
Theorem: given enough mixtures of generator and discriminators, the generator can approximately win the game.

MIX+GAN: Mixture of generators and discriminators

Following the theoretical analysis, the paper proposes to use mixture of generators and mixture of discriminators. The objective is to minimize $T$ generators and their mixture weights, and $T$ discriminators and their mixture weights.
Here $w = \mathrm{softmax}(\alpha)$

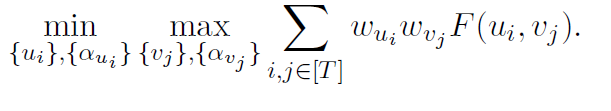
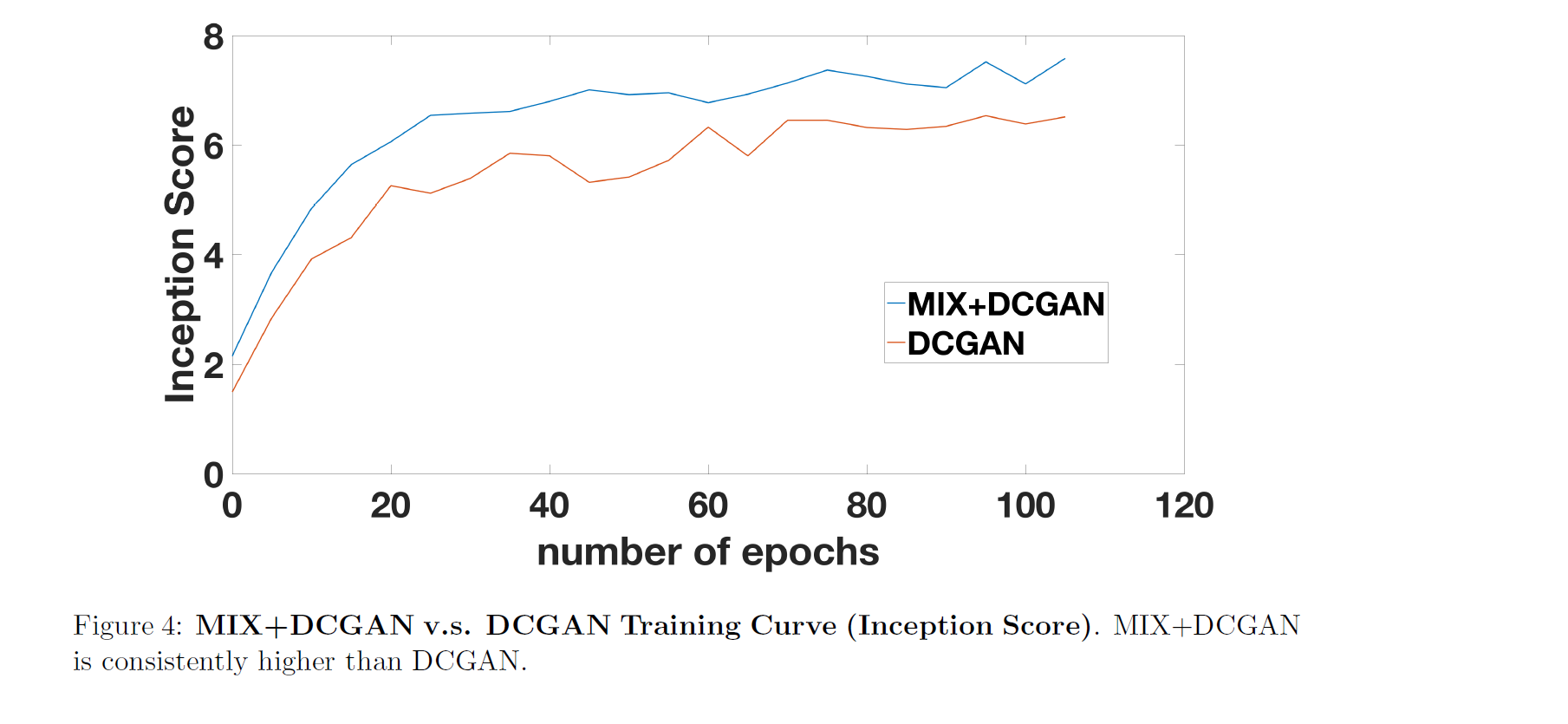
The paper uses DCGAN[3] as the base model and shows that MIX+DCGAN generates better looking images and has higher inception score than DCGAN.

Wasserstein GAN training with gradient penalty (Paper 2)

The paper is based on the nice result that the optimal discriminator (called “critic” in the paper) has gradients with norm 1 almost everywhere. Here the gradient is with respect to $x$, not the parameter of the discriminator.

Gradient Clipping does not work very well for the following reasons.

1. The optimizer with gradient clipping searches the discriminator in a space smaller than 1-Lipschitz, so it biases the discriminator toward simpler functions.
2. Clipped gradients vanish or explode as they back-propagate through network layers.

The theoretical result of the gradient and the drawback of gradient clipping motivates their new method, “gradient penalty.” The discriminator gets a penalty if the norm of its gradient is not one. The objective is

$\hat{x}$ is a random point lying on the line between $x$ and $\tilde{x}$.

In the experiment, GAN training with gradient penalties has faster convergence speed than that with weight clipping. In the image generation and language modeling task, the models trained with the proposed method often gives better results than competing methods.

References

[1] Arora, Sanjeev, et al. “Generalization and Equilibrium in Generative Adversarial Nets (GANs).” arXiv preprint arXiv:1703.00573 (2017).

[2] Gulrajani, Ishaan, et al. “Improved Training of Wasserstein GANs.” arXiv preprint arXiv:1704.00028 (2017).

[3] Radford, Alec, et al. “Unsupervised representation learning with deep convolutional generative adversarial networks”. In International Conference on Learning Representations, 2016.